快速排序和堆排序

快速排序
堆排序

快速排序

我们知道冒泡排序、插入排序、选择排序这三种排序算法，它们的时间复杂度都是O(n²)，比较高，只适合小规模的排序。归并排序和快速排序，是时间复杂度为O(nlogn)的排序算法，这两种排序算法就比较适合大规模的数据排序，且它们都用到了分治思想。

在实际的工程项目中，快排是最常用到的一种排序算法，所以本文将重点介绍快排。

快排的原理

快速排序算法（Quick Sort），我们习惯性把它简称为“快排”，快排利用的也是分治思想。我们先来看下快排的核心思想。快排的思想是这样的：

如果要排序数组中下标从 p 到 r 之间的一组数据，我们选择 p 到 r 之间的任意一个数据作为 pivot（分区点）。我们遍历 p 到 r 之间的数据，将小于 pivot 的放到左边，将大于 pivot 的放到右边，将 pivot 放到中间。经过这一步骤之后，数组 p 到 r 之间的数据就被分成了三个部分，前面 p 到 q-1 之间都是小于 pivot 的，中间是 pivot，后面的 q+1 到 r 之间是大于 pivot 的。

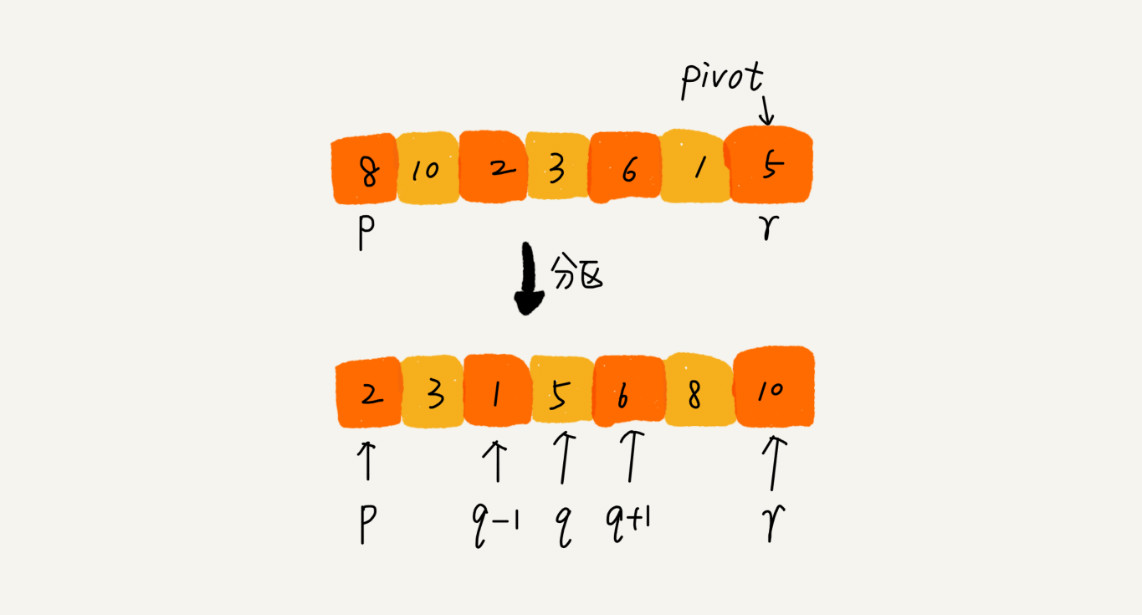
根据分治的处理思想，我们可以用递归来排序下标从 p 到 q-1 之间的数据和下标从 q+1 到 r 之间的数据，直到区间缩小为 1，就说明所有的数据都有序了。

可用递推公式来表示上述过程：

递推公式：quick_sort(p…r) = quick_sort(p…q-1) + quick_sort(q+1… r)
终止条件：p >= r

伪代码如下：

// 快速排序，A是数组，n表示数组的大小
quick_sort(A, n) { 
  quick_sort_c(A, 0, n-1)
}
// 快速排序递归函数，p,r为下标
quick_sort_c(A, p, r) {
  if p >= r then return
  
  q = partition(A, p, r) // 获取分区点 
  quick_sort_c(A, p, q-1) 
  quick_sort_c(A, q+1, r)
}

partition()是一个分区函数，它的主要功能就是随机选择一个元素作为 pivot 分区点（一般情况下，可以选择 p 到 r 区间的最后一个元素），然后对 A[p…r]分区，函数返回 pivot 的下标。

如果我们不考虑空间消耗的话，partition() 分区函数可以写得非常简单。我们申请两个临时数组 X 和 Y，遍历 A[p…r]，将小于 pivot 的元素都拷贝到临时数组 X，将大于 pivot 的元素都拷贝到临时数组 Y，最后再将数组 X 和数组 Y 中数据顺序拷贝到 A[p….r]原数组中。

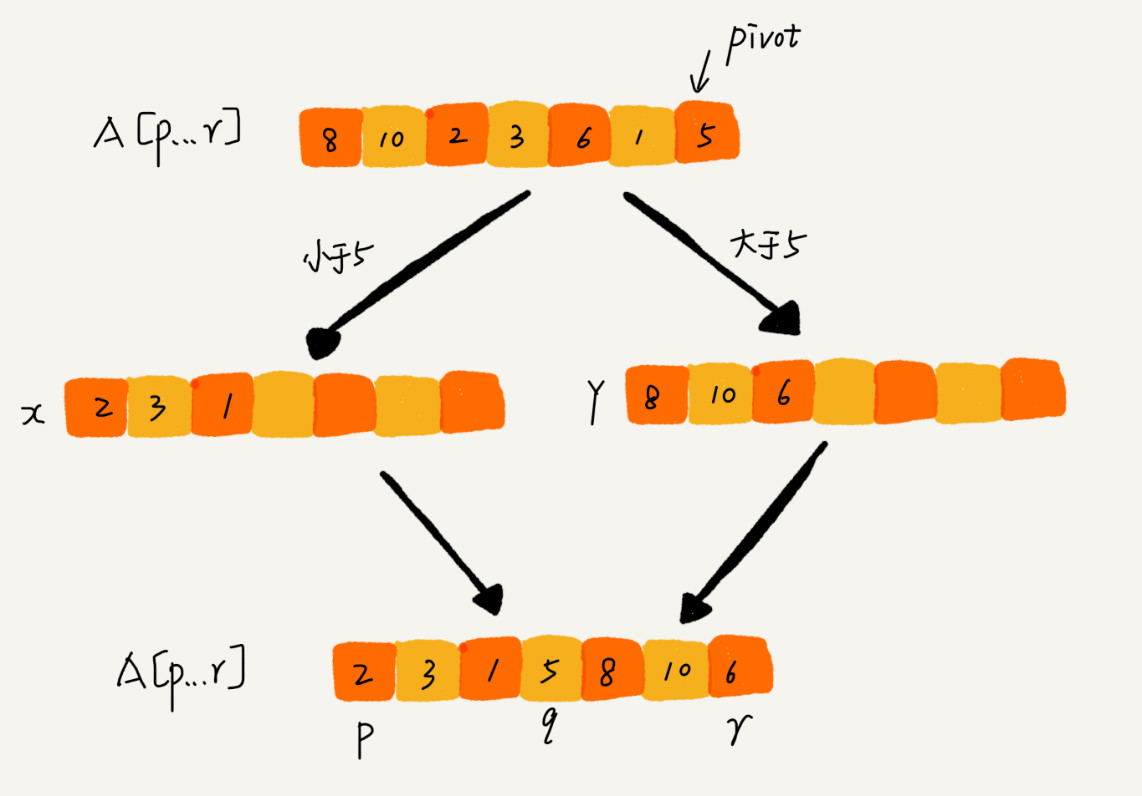
但是，如果按照这种思路实现的话，partition() 函数就需要很多额外的内存空间，所以快排就不是原地排序算法了。如果我们希望快排是原地排序算法，那它的空间复杂度得是 O(1)，那 partition() 分区函数就不能占用太多额外的内存空间，我们就需要在 A[p…r]的原地完成分区操作。

原地分区函数的实现思路非常巧妙，伪代码参考如下：

partition(A, p, r) { 
  pivot := A[r] 
  i := p 
  for j := p to r-1 do { 
    if A[j] < pivot { 
        swap A[i] with A[j] 
        i := i+1 
    } 
  } 
  swap A[i] with A[r] 
  return i

这里的处理有点类似选择排序。我们通过游标 i 把 A[p…r-1]分成两部分。A[p…i-1]的元素都是小于 pivot 的，我们暂且叫它“已处理区间”，A[i…r-1]是“未处理区间”。我们每次都从未处理的区间 A[i…r-1]中取一个元素 A[j]，与 pivot 对比，如果小于 pivot，则将其加入到已处理区间的尾部，也就是 A[i]的位置。

类似于数组的插入操作，在数组某个位置插入元素，需要搬移数据，非常耗时。我们会用到一种处理技巧，就是交换，在 O(1) 的时间复杂度内完成插入操作。这里我们也借助这个思想，只需要将 A[i]与 A[j]交换，就可以在 O(1) 时间复杂度内将 A[j]放到下标为 i 的位置。

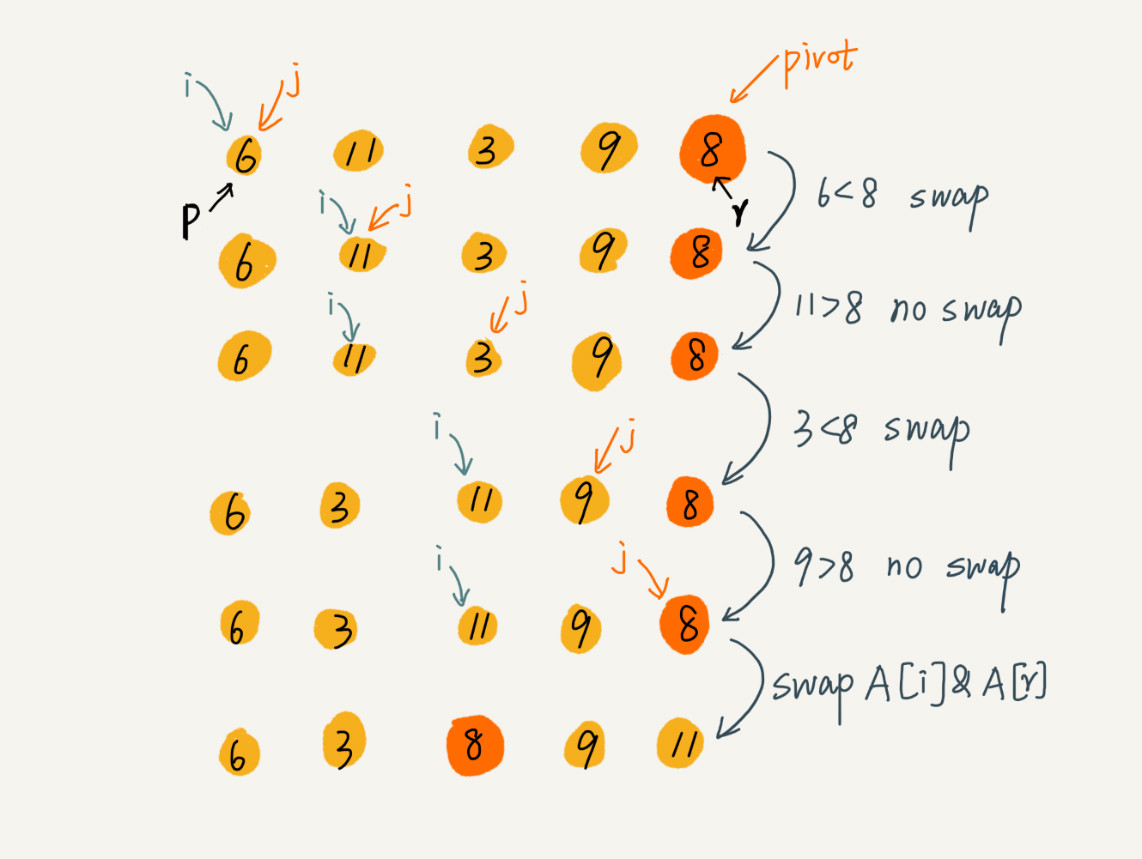
因为分区的过程涉及交换操作，如果数组中有两个相同的元素，比如序列 6，8，7，6，3，5，9，4，在经过第一次分区操作之后，两个 6 的相对先后顺序就会改变。所以，快速排序并不是一个稳定的排序算法。

快排与归并的区别

快排和归并用的都是分治思想，递推公式和递归代码也非常相似，那它们的区别在哪里呢？

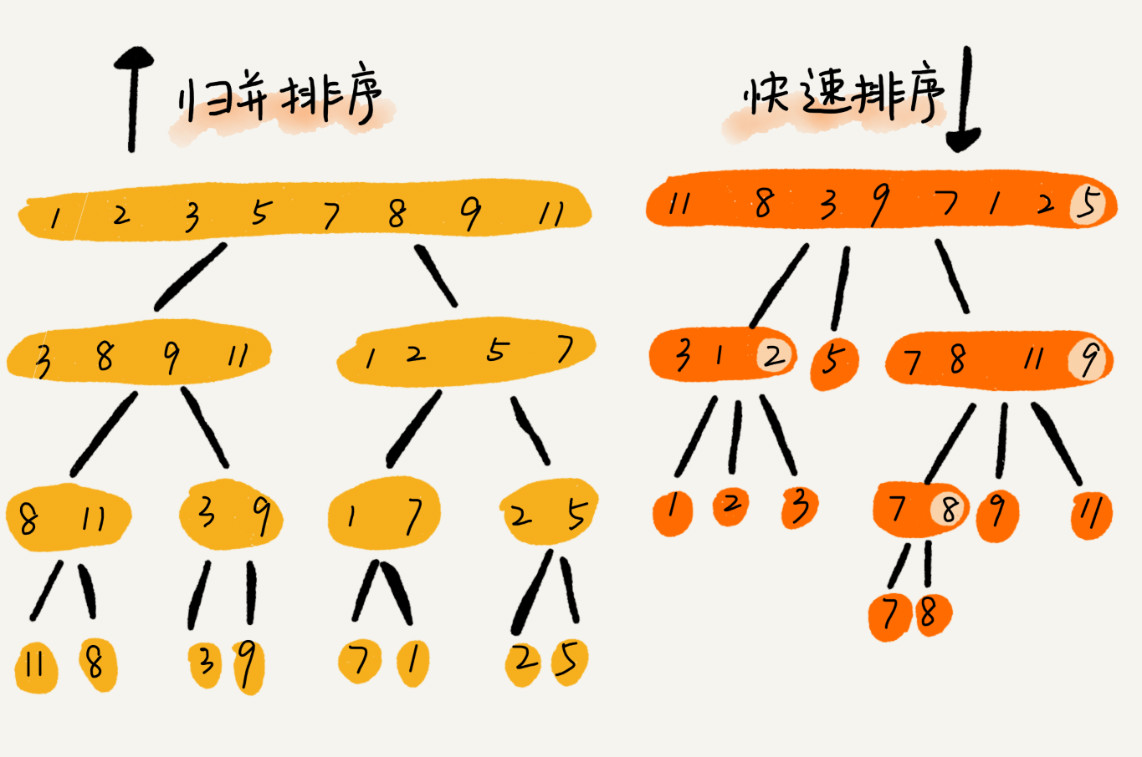
可以发现，归并排序的处理过程是由下到上的，先处理子问题，然后再合并。而快排正好相反，它的处理过程是由上到下的，先分区，然后再处理子问题。归并排序虽然是稳定的、时间复杂度为 O(nlogn) 的排序算法，但是它是非原地排序算法。归并之所以是非原地排序算法，主要原因是合并函数无法在原地执行。快速排序通过设计巧妙的原地分区函数，可以实现原地排序，解决了归并排序占用太多内存的问题。

快排的性能分析

在上文中，已经分析了快排的稳定性和空间复杂度。快排是原地、不稳定的排序算法。

快排也是用递归来实现的。对于递归代码的时间复杂度，如果每次分区操作，都能正好把数组分成大小接近相等的两个小区间，那快排的时间复杂度递推求解公式跟归并是相同的。所以，快排的时间复杂度也是 O(nlogn)。

T(1) = C； n=1时，只需要常量级的执行时间，所以表示为C。
T(n) = 2*T(n/2) + n； n>1

但是，公式成立的前提是每次分区操作，我们选择的 pivot 都很合适，正好能将大区间对等地一分为二。但实际上这种情况是很难实现的。

举一个比较极端的例子。如果数组中的数据原来已经是有序的了，比如 1，3，5，6，8。如果我们每次选择最后一个元素作为 pivot，那每次分区得到的两个区间都是不均等的。我们需要进行大约 n 次分区操作，才能完成快排的整个过程。每次分区我们平均要扫描大约 n/2 个元素，这种情况下，快排的时间复杂度就从 O(nlogn) 退化成了 O(n²)。

刚刚讲了两个极端情况下的时间复杂度，一个是分区极其均衡，一个是分区极其不均衡。它们分别对应快排的最好情况时间复杂度和最坏情况时间复杂度。那快排的平均情况时间复杂度是多少呢？

结论是：快排时间复杂度 T(n) 在大部分情况下的时间复杂度都可以做到 O(nlogn)，只有在极端情况下，才会退化到 O(n²)。

思考题—O(n) 时间复杂度内求无序数组中的第 K 大元素

O(n) 时间复杂度内求无序数组中的第 K 大元素？比如，4， 2， 5， 12， 3 这样一组数据，第 3 大元素就是 4。

我们选择数组区间 A[0…n-1]的最后一个元素 A[n-1]作为 pivot，对数组 A[0…n-1]原地分区，这样数组就分成了三部分，A[0…p-1]、A[p]、A[p+1…n-1]。

如果 p+1=K，那 A[p]就是要求解的元素；如果 K>p+1, 说明第 K 大元素出现在 A[p+1…n-1]区间，我们再按照上面的思路递归地在 A[p+1…n-1]这个区间内查找。同理，如果 K<p+1，那我们就在A[0…p-1]区间查找。

第一次分区查找，我们需要对大小为 n 的数组执行分区操作，需要遍历 n 个元素。第二次分区查找，我们只需要对大小为 n/2 的数组执行分区操作，需要遍历 n/2 个元素。依次类推，分区遍历元素的个数分别为、n/2、n/4、n/8、n/16.……直到区间缩小为 1。

如果我们把每次分区遍历的元素个数加起来，就是：n+n/2+n/4+n/8+…+1。这是一个等比数列求和，最后的和等于 2n-1。所以，上述解决思路的时间复杂度就为 O(n)。

堆排序

堆的定义

堆是一种特殊的树，什么样的树才是堆呢？

堆是一个完全二叉树；

堆中每一个节点的值都必须大于等于（或小于等于）其子树中每个节点的值。

分别解释一下这两点。

第一点，堆必须是一个完全二叉树。完全二叉树要求，除了最后一层，其他层的节点个数都是满的，最后一层的节点都靠左排列。

第二点，堆中的每个节点的值必须大于等于（或者小于等于）其子树中每个节点的值。实际上，我们还可以换一种说法，堆中每个节点的值都大于等于（或者小于等于）其左右子节点的值。这两种表述是等价的。

对于每个节点的值都大于等于子树中每个节点值的堆，我们叫做“大顶堆”。对于每个节点的值都小于等于子树中每个节点值的堆，我们叫做“小顶堆”。

堆的实现

要实现一个堆，首先要知道，堆都支持哪些操作以及如何存储一个堆。

我们知道完全二叉树比较适合用数组来存储，用数组来存储完全二叉树是非常节省存储空间的，因为我们不需要存储左右子节点的指针，单纯地通过数组的下标，就可以找到一个节点的左右子节点和父节点。

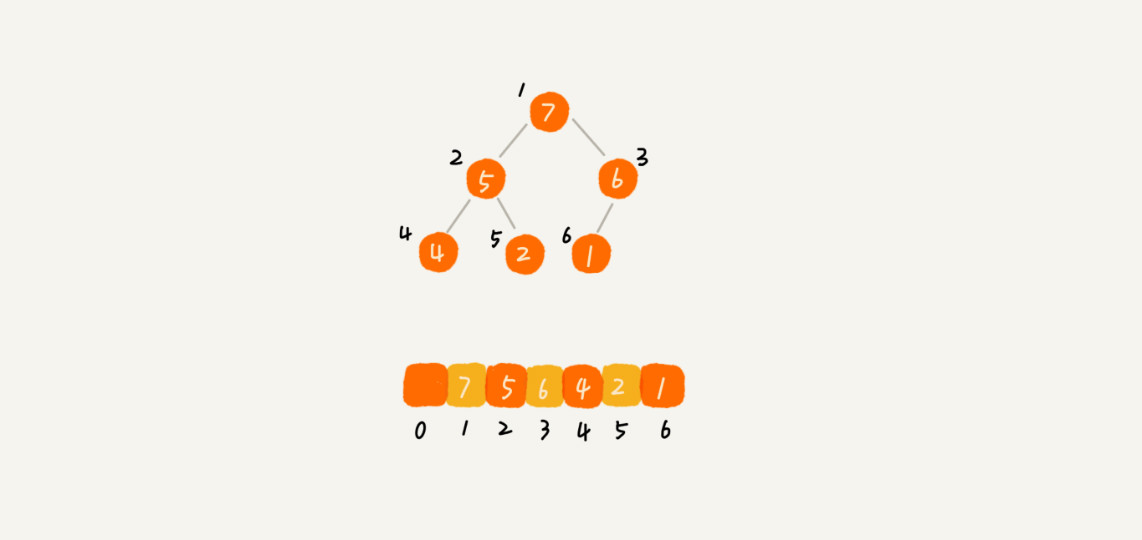
从图中我们可以看到，数组中下标为 i 的节点的左子节点，就是下标为 i∗2 的节点，右子节点就是下标为 i∗2+1 的节点，父节点就是下标为 2/i 的节点。

堆排序

常见的排序算法有时间复杂度是 O(n²) 的冒泡排序、插入排序、选择排序，有时间复杂度是 O(nlogn) 的归并排序、快速排序，还有线性排序。

这里我们借助于堆这种数据结构实现的排序算法，就叫做堆排序。这种排序方法的时间复杂度非常稳定，是 O(nlogn)，并且它还是原地排序算法。如此优秀，它是怎么做到的呢？

我们可以把堆排序的过程大致分解成两个大的步骤，建堆和排序。

1. 建堆

我们首先将数组原地建成一个堆。“原地”就是不借助另一个数组，就在原数组上操作。建堆的过程，有两种思路。

第一种是类似在堆中插入一个元素的思路。尽管数组中包含 n 个数据，但是我们可以假设，起初堆中只包含一个数据，就是下标为 1 的数据。然后，我们调用前面堆的插入操作，将下标从 2 到 n 的数据依次插入到堆中。这样我们就将包含 n 个数据的数组，组织成了堆。

第二种实现思路，跟第一种截然相反。第一种建堆思路的处理过程是从前往后处理数组数据，并且每个数据插入堆中时，都是从下往上堆化。而第二种实现思路，是从后往前处理数组，并且每个数据都是从上往下堆化。

下图是第二种实现思路的建堆分解步骤图。因为叶子节点往下堆化只能自己跟自己比较，所以直接从最后一个非叶子节点开始，依次堆化即可。

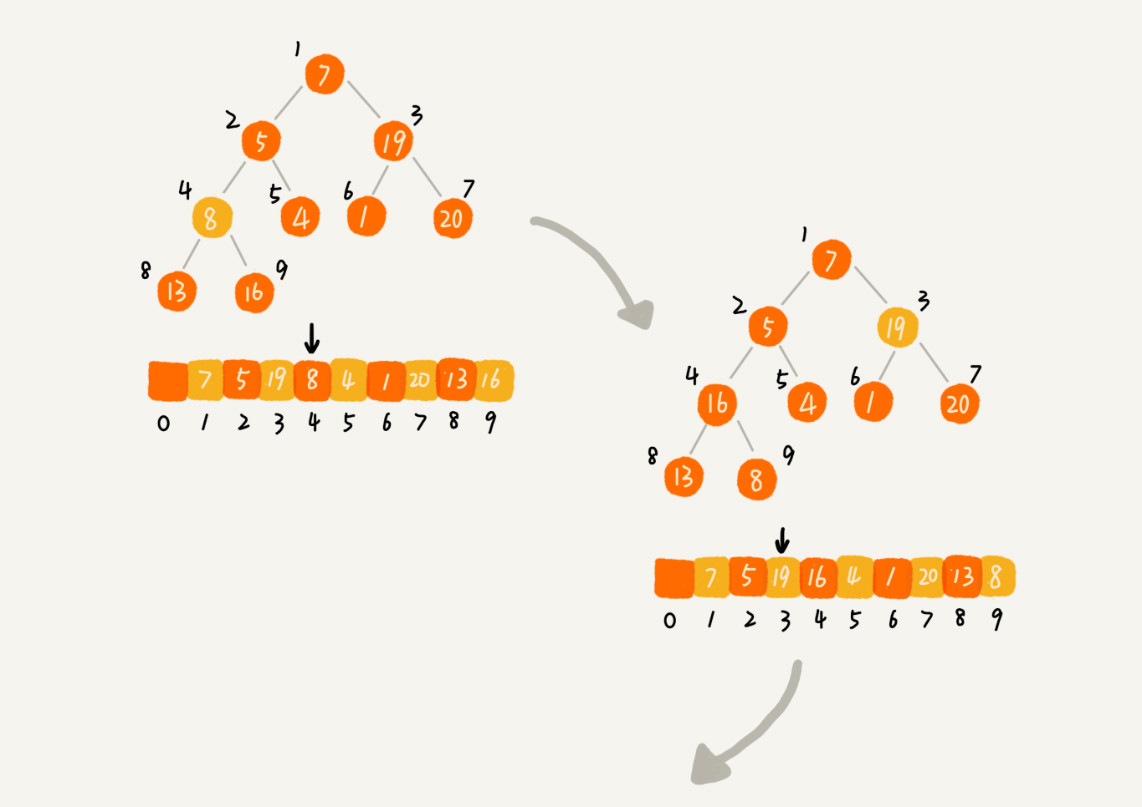
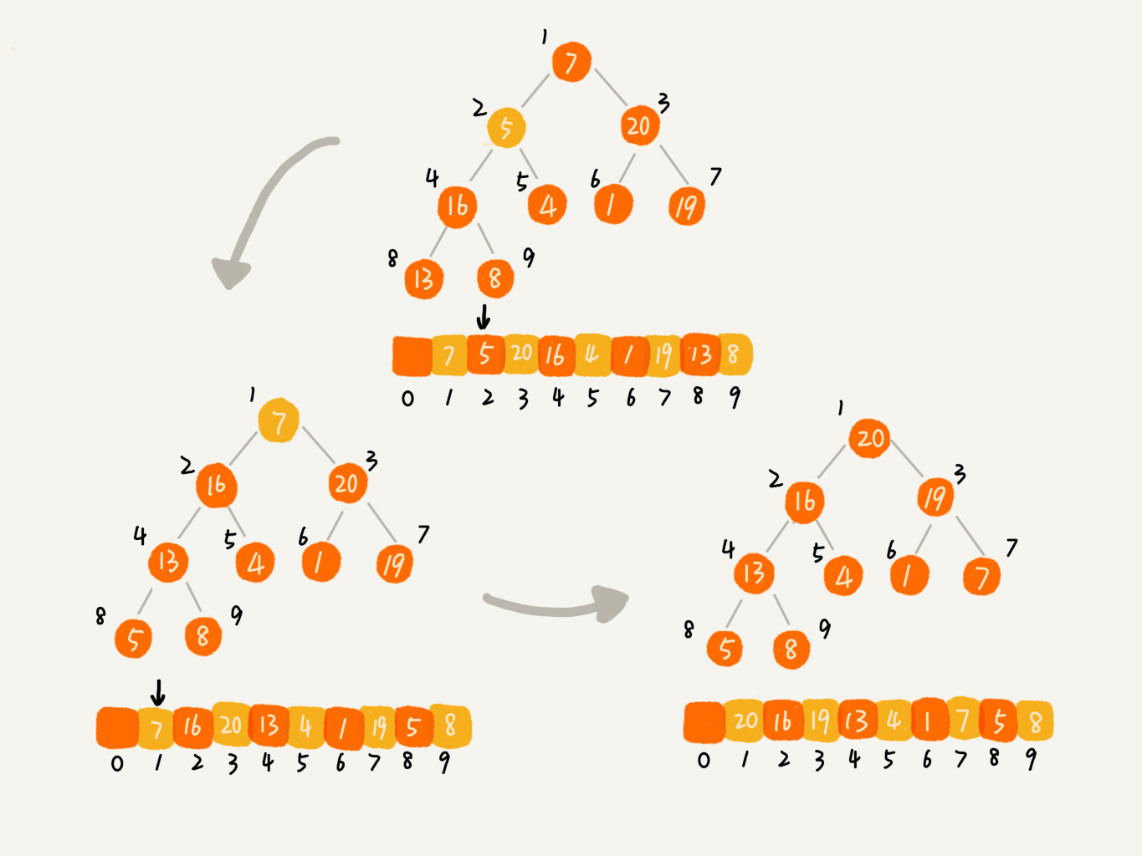
实现代码如下：

private static void buildHeap(int[] a, int n) {
    for (int i = n/2; i >= 1; --i) {  // n/2为第一个非叶子节点
        heapify(a, n, i);
    }
}

private static void heapify(int[] a, int n, int i) {
    while (true) {
        int maxPos = i;
        if (i*2 <= n && a[i] < a[i*2]) maxPos = i*2; //左子节点更大
        if (i*2+1 <= n && a[maxPos] < a[i*2+1]) maxPos = i*2+1; //右子节点更大
        if (maxPos == i) break; //本节点最大
        swap(a, i, maxPos); //交换父节点与最大子节点位置
        i = maxPos;
    }
}

注：

对下标从 1 开始到 n/2 的数据进行堆化，下标是 n/2+1 到 n 的节点是叶子节点，不需要堆化。对于完全二叉树来说，下标从 n/2+1 到 n 的节点都是叶子节点。
建堆操作的时间复杂度就是 O(n)。

2. 排序

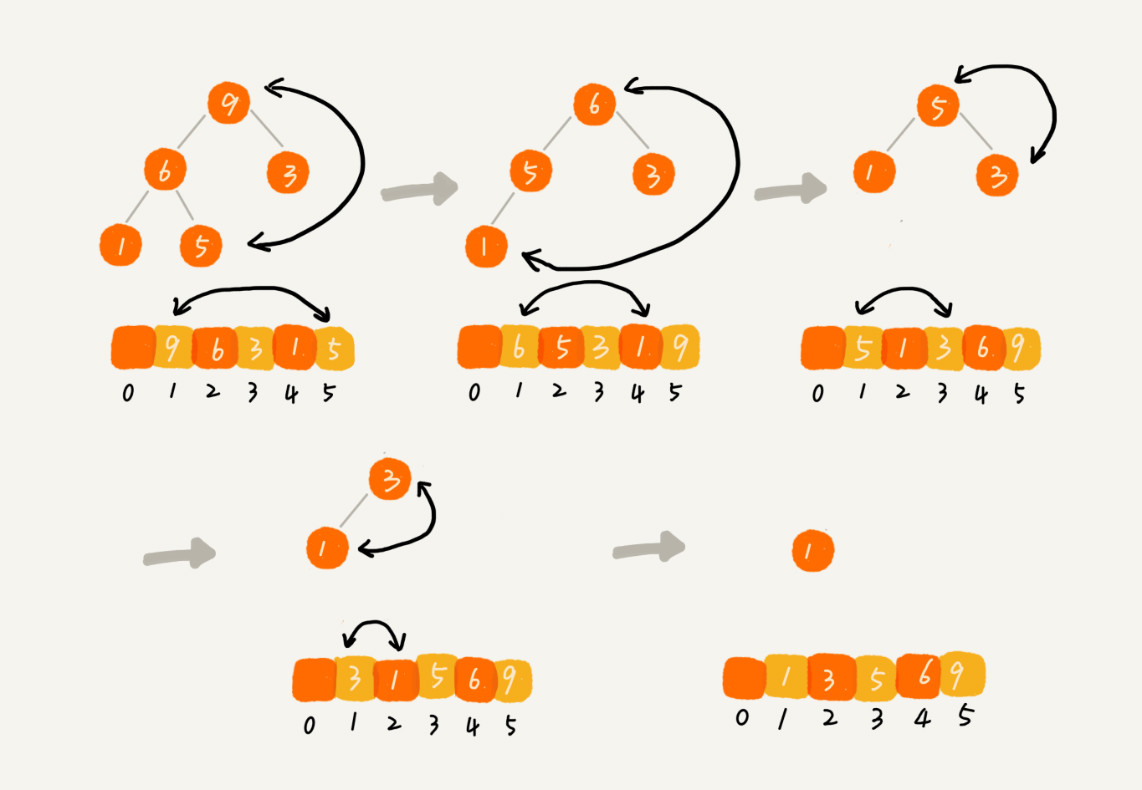
建堆结束之后，数组中的数据已经是按照大顶堆的特性来组织的。数组中的第一个元素就是堆顶，也就是最大的元素。我们把它跟最后一个元素交换，那最大元素就放到了下标为 n 的位置。

这个过程有点类似删除堆顶元素的操作，当堆顶元素移除之后，我们把下标为 n 的元素放到堆顶，然后再通过堆化的方法，将剩下的 n−1 个元素重新构建成堆。堆化完成之后，我们再取堆顶的元素，放到下标是 n−1 的位置，一直重复这个过程，直到最后堆中只剩下标为 1 的一个元素，排序工作就完成了。

实现代码如下

// n表示数据的个数，数组a中的数据从下标1到n的位置。
public static void sort(int[] a, int n) {
    buildHeap(a, n);
    int k = n;
    while (k > 1) {
        swap(a, 1, k);
        --k;
        heapify(a, k, 1);
    }
}

整个堆排序的过程，都只需要极个别临时存储空间，所以堆排序是原地排序算法。堆排序包括建堆和排序两个操作，建堆过程的时间复杂度是 O(n)，排序过程的时间复杂度是 O(nlogn)，所以，堆排序整体的时间复杂度是 O(nlogn)。

堆排序不是稳定的排序算法，因为在排序的过程，存在将堆的最后一个节点跟堆顶节点互换的操作，所以就有可能改变值相同数据的原始相对顺序。

思考题—实际开发中，为什么快速排序要比堆排序性能好？

主要原因有二：

第一点，堆排序数据访问的方式没有快速排序友好。

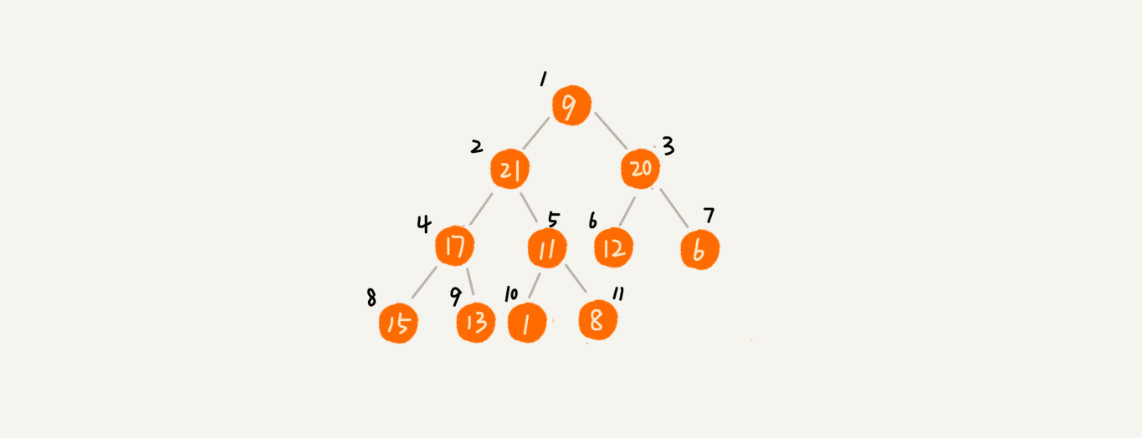
对于快速排序来说，数据是顺序访问的。而对于堆排序来说，数据是跳着访问的。比如，堆排序中，最重要的一个操作就是数据的堆化。比如下面这个例子，对堆顶节点进行堆化，会依次访问数组下标是 1，2，4，8 的元素，而不是像快速排序那样，局部顺序访问，所以，这样对 CPU 缓存是不友好的。

第二点，对于同样的数据，在排序过程中，堆排序算法的数据交换次数要多于快速排序。

排序有两个重要概念，有序度和逆序度。对于基于比较的排序算法来说，整个排序过程就是由两个基本的操作组成的，比较和交换（或移动）。快速排序数据交换的次数不会比逆序度多。

但是堆排序的第一步是建堆，建堆的过程会打乱数据原有的相对先后顺序，导致原数据的有序度降低。比如，对于一组已经有序的数据来说，经过建堆之后，数据反而变得更无序了。