1. Paxos定义
Paxos算法是莱斯利·兰伯特(英语:Leslie Lamport)于1990年提出的一种基于消息传递且具有高度容错特性的共识(consensus)算法。
注意:Paxos常被误称为“一致性算法”。但是“一致性算法”和“共识算法”并非同一个概念,详见:分布式系统的一致性和共识性
2. 提出背景
分布式系统中的节点通信存在两种模型:共享内存(Shared memory)和消息传递(Messages passing)。基于消息传递通信模型的分布式系统,不可避免的会发生以下错误:进程运行缓慢、被杀死或者重启,消息可能会出现延迟、丢失、重复。在基础 Paxos 场景中,先不考虑可能出现消息篡改即拜占庭错误的情况。Paxos 算法解决的问题是在一个可能发生上述异常的分布式系统中如何就某个值达成一致(注意:值并不只是狭义上的某个数,它可以是一条日志,也可以是一条命令(command)。根据应用场景不同,值有不同的含义),保证不论发生以上任何异常,都不会破坏决议的共识。一个典型的场景是,在一个分布式数据库系统中,如果各节点的初始状态一致,每个节点都执行相同的操作序列,那么他们最后能得到一个一致的状态。为保证每个节点执行相同的命令序列,需要在每一条指令上执行一个“共识算法”以保证每个节点看到的指令一致。
3. 算法概述
3.1 相关概念
在Paxos算法中,定义了三种角色:
- Proposer
- Acceptotr
- Learners
注:一个进程可能同时充当多种角色。比如一个进程可能既是Proposer又是Acceptor又是Learner
Proposers提出提案,提案信息包括提案编号和提议的某个值(value);Acceptor收到提案后可以接受(accept)提案,若提案获得多数派(majority)的Acceptors的接受,则称该提案被批准(chosen);Learners只能”学习”被批准的提案。划分角色后,就可以进一步精确定义问题:
- 决议(value)只有在被Proposers提出后才能被批准(未经批准的决议称为“提案(proposal)”);
- 在一次Paxos算法的执行实例中,只批准(chosen)一个value;
- Learners只能获得被批准(chosen)的value。
在 Leslie Lamport 之后发表的paper中将 majority 替换为更通用的 quorum 概念,但在
描述classic paxos的论文 Paxos made simple 中使用的还是 majority 的概念。 作者通过不断加强上述3个约束(**主要是第二个**)获得了 Paxos 算法。 批准 value 的过程中,首先 Proposers 将 value 发送给 Acceptors,之后 Acceptors 对 value 进行接受(accept)。为了满足只批准一个 value 的约束,要求经“多数派(majority)”接受的 value 成为正式的决议(称为“批准”决议)。这是因为无论是按照人数还是按照权重划分,两组“多数派”**至少有一个公共的 Acceptor**,如果每个 Acceptor 只能接受一个 value,约束2就能保证。
3.2 算法推导
最简单的方案——只有一个Acceptor
假设只有一个Acceptor(可以有多个Proposer),只要Acceptor接受它收到的第一个提案,则该提案就被批准,该提案里的value就是被选定的value,这也保证了只有一个value会被批准。
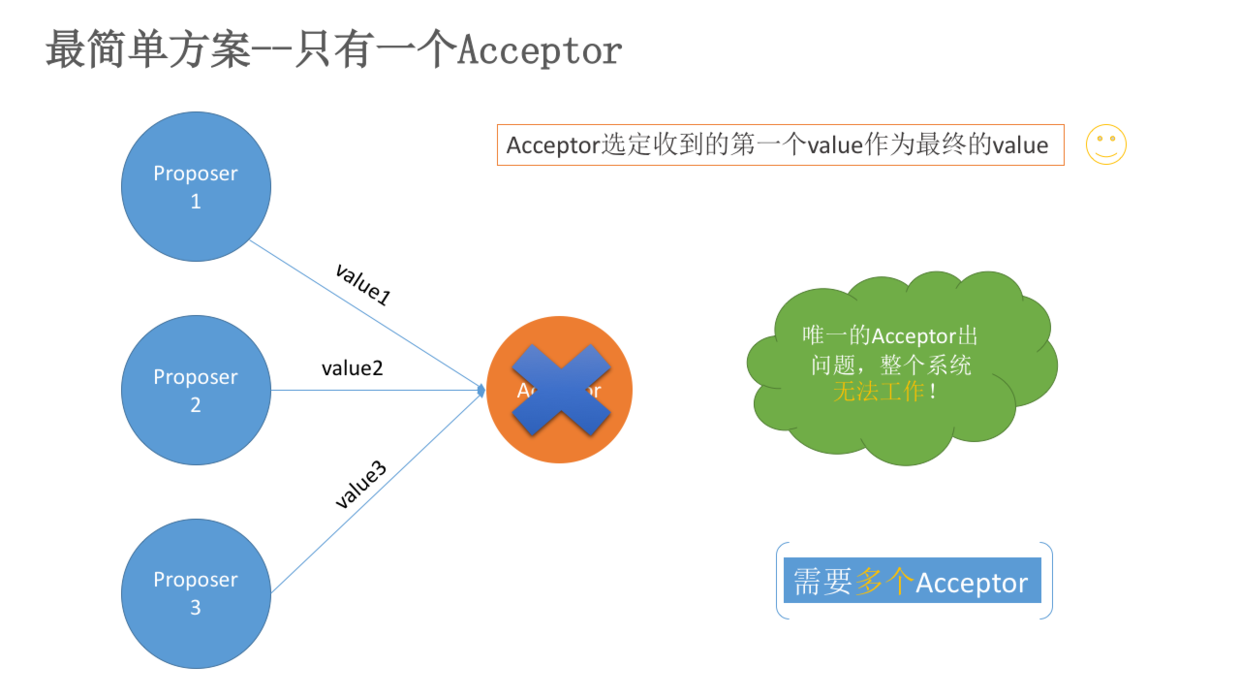
但是,这存在单点问题,即如果这个唯一的Acceptor宕机了,那么整个系统就无法工作了。
因此,此方案虽然实现简单,但一个稳定的系统必须要有多个Acceptor。
多个Acceptor
多个Acceptor的情况如下图。那么,如何保证在多个Proposer和多个Acceptor的情况下选定一个value呢?
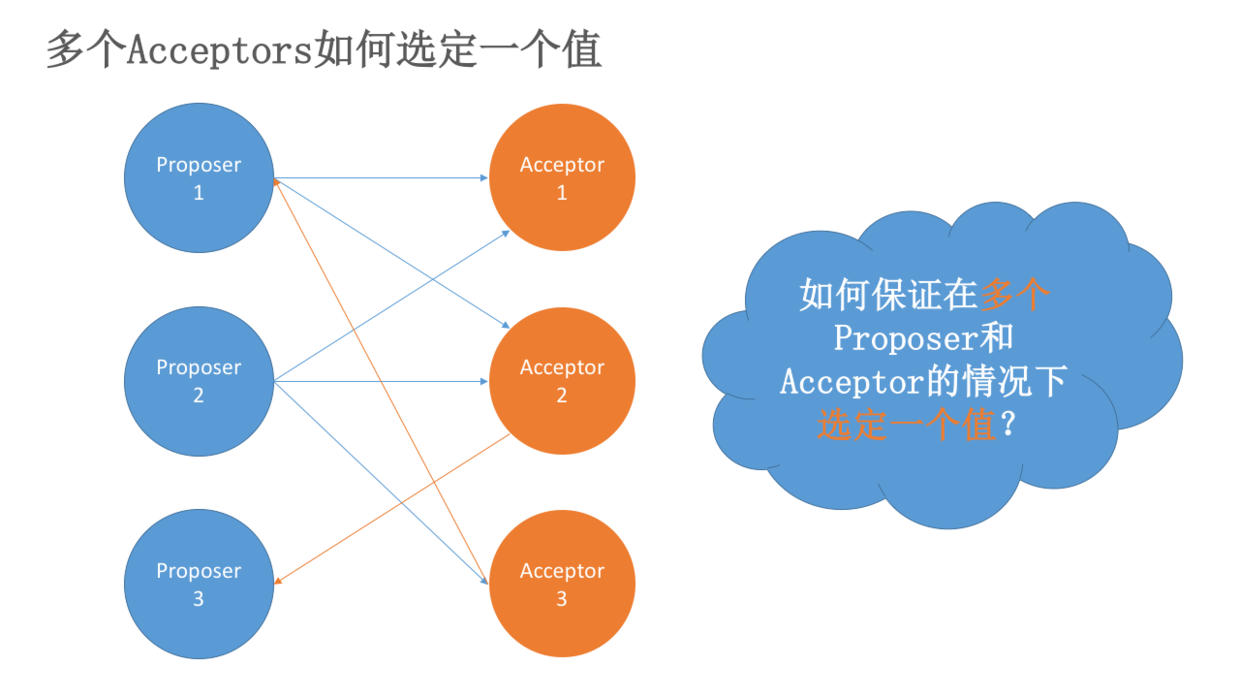
推导过程
如果我们希望即使只有一个Proposer提出了一个value,该value也最终被选定。
那么,就得到下面的约束:
P1:一个Acceptor必须接受它收到的第一个提案。
但是,这又会引出另一个问题:如果每个Proposer分别提出不同的value,发给不同的Acceptor。根据P1,Acceptor分别接受自己收到的value,就导致不同的value被选定。出现了不一致。如下图:
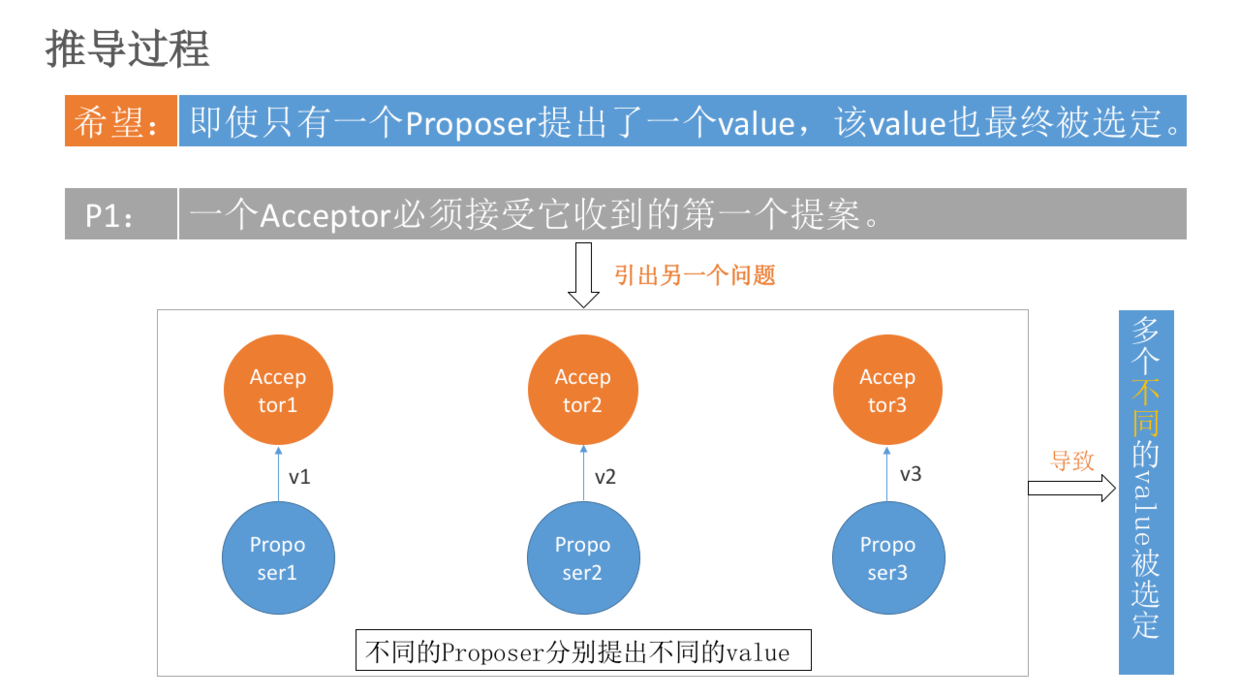
因此,我们需要加一个规定:
规定:一个提案被批准需要被半数以上的Acceptor接受。
这个规定又暗示了:一个Acceptor必须能够接受不止一个提案。不然可能导致最终没有value被选定。比如上图的情况。v1、v2、v3都没有被选定,因为它们都只被一个Acceptor的接受。
虽然允许了多个提案被选定,但必须要保证所有被选定的提案都具有相同的value值,否则又会出现不一致的情况。
于是有了下面的约束:
P2:一旦一个具有 value v 的提案被批准(chosen),那么之后每个编号更高的被批准(chosen)的提案必须也是 value v。
注:通过某种方法可以为每个提案分配一个编号,在提案之间建立一个全序关系,所谓“之后”都是指所有编号更大的提案。
如果 P1 和 P2 都能够保证,那么约束2就能够保证,即一次Paxos算法的执行实例中,只批准(chosen)一个value。
批准一个 value 意味着多个 Acceptor 接受(accept)了该 value。因此,可以对 P2 进行加强:
P2a:一旦一个具有 value v 的提案被批准(chosen),那么之后任何 Acceptor 再次接受(accept)的提案必须也是 value v。
由于通信是异步的,P2a 和 P1 会发生冲突。如果一个 value 被批准后,一个 Proposer 和一个 Acceptor 从休眠中苏醒,前者提出一个具有新的 value 的提案。根据 P1,后者应当接受,根据 P2a,则不应当接受,这种场景下 P2a 和 P1 有矛盾。
假设总的有5个Acceptor。Proposer2提出[M1,V1]的提案,Acceptor2~5(半数以上)均接受了该提案,于是对于Acceptor2~5和Proposer2来讲,它们都认为V1被选定。Acceptor1刚刚从宕机状态恢复过来(之前Acceptor1没有收到过任何提案),此时Proposer1向Acceptor1发送了[M2,V2]的提案(V2≠V1且M2>M1),对于Acceptor1来讲,这是它收到的第一个提案。根据P1(一个Acceptor必须接受它收到的第一个提案。),Acceptor1必须接受该提案!同时Acceptor1认为V2被选定。这就出现了两个问题:
- Acceptor1认为V2被选定,Acceptor2~5和Proposer2认为V1被选定。出现了不一致
- V1被选定了,但是编号更高的被Acceptor1接受的提案[M2,V2]的value为V2,且V2≠V1。这就跟P2a(如果某个value为v的提案被选定了,那么每个编号更高的被Acceptor接受的提案的value必须也是v)矛盾了。
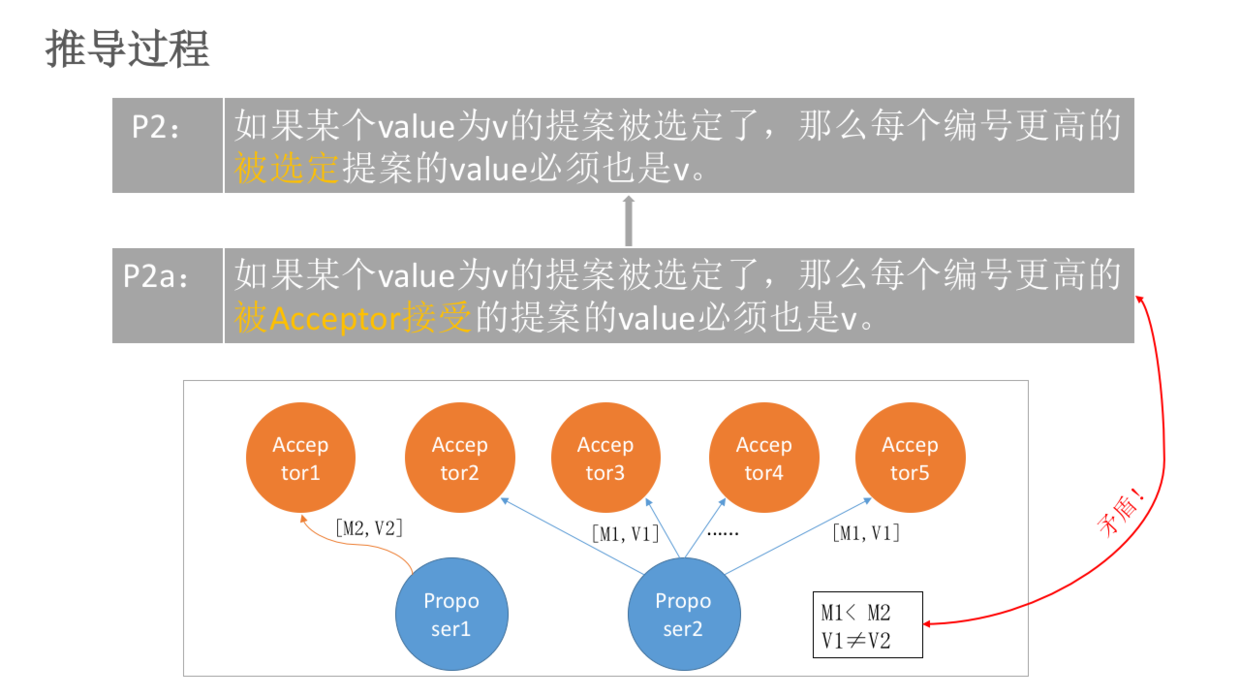
所以我们要对P2a约束进行强化!
P2a是对Acceptor接受的提案约束,但其实提案是Proposer提出来的,所有我们可以对Proposer提出的提案进行约束。得到P2b:
P2b:一旦一个具有 value v 的提案被批准(chosen),那么以后任何 Proposer 提出的提案必须具有 value v。
由P2b可以推出P2a进而推出P2。
那么,如何确保在某个value为v的提案被选定后,Proposer提出的编号更高的提案的value都是v呢?
只要满足P2c即可:
P2c:如果一个编号为 n 的提案具有 value v,该提案被提出(issued),那么存在一个多数派,要么他们中所有人都没有接受(accept)编号小于 n 的任何提案,要么他们已经接受(accept)的所有编号小于 n 的提案中编号最大的那个提案具有 value v。
通过数学归纳法,可以证明若满足P2c,则P2b一定满足。
P2c是可以通过消息传递模型实现的。
3.3 算法内容
Proposer生成提案之前,应该先去『学习』已经被选定或者可能被选定的value,然后以该value作为自己提出的提案的value。如果没有value被选定,Proposer才可以自己决定value的值,这样才能达成一致。这个学习的阶段是通过一个『Prepare请求』实现的。当获得多数acceptors接受(accept)后,提案获得批准(chosen),由Acceptor将这个消息告知Learner。
如果一个没有chosen过任何Proposer提案的Acceptor在prepare过程中回答了一个Proposer针对提案n的问题,但是在开始对n进行投票前,又接受(accept)了编号小于n的另一个提案(例如n-1),如果n-1和n具有不同的value,这个投票就会违背P2c。因此在prepare过程中,acceptor进行的回答同时也应包含承诺:不会再接受(accept)编号小于n的提案。这是对P1的加强:
P1a:当且仅当Acceptor没有响应过编号大于n的prepare请求时,Acceptor接受(accept)编号为n的提案。
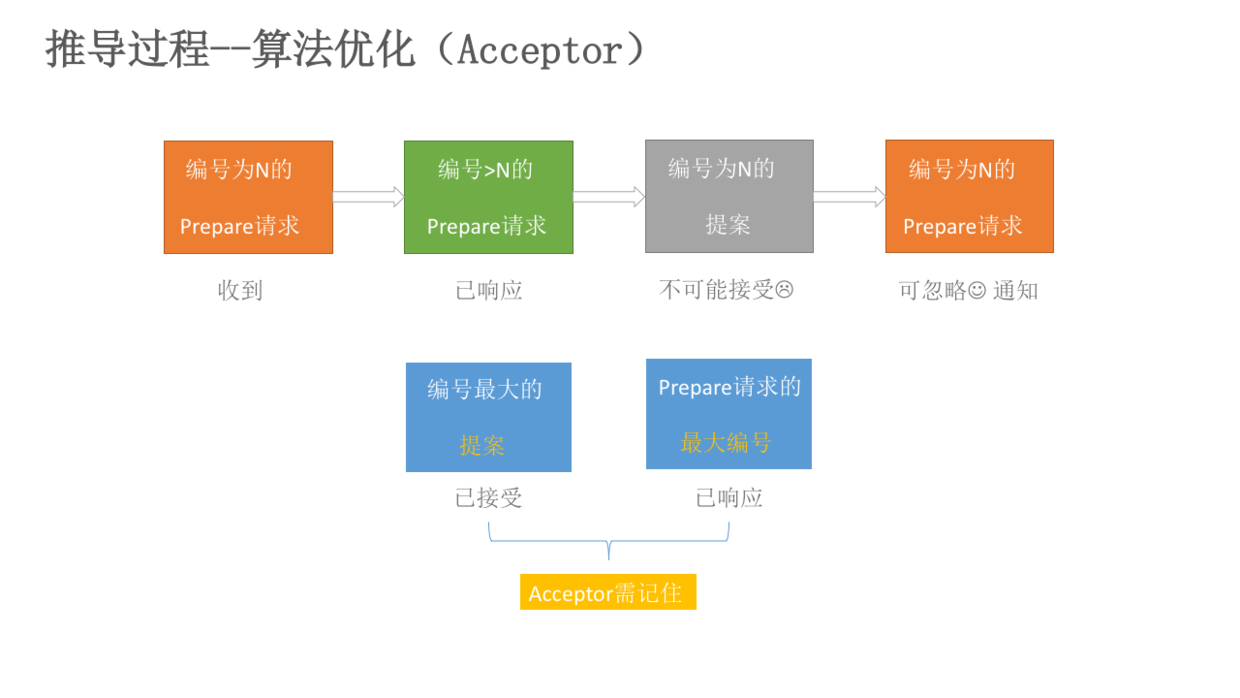
如果Acceptor收到一个编号为n的Prepare请求,在此之前它已经响应过编号大于n的Prepare请求。根据P1a,该Acceptor不可能接受编号为n的提案。因此,该Acceptor可以忽略编号为N的Prepare请求。当然,也可以回复一个error,让Proposer尽早知道自己的提案不会被接受。
因此,一个Acceptor只需记住:. 已接受的编号最大的提案 2. 已响应的请求的最大编号。
如果Acceptor收到一个编号为N的Prepare请求,在此之前它已经响应过编号大于N的Prepare请求。根据P1a,该Acceptor不可能接受编号为N的提案。因此,该Acceptor可以忽略编号为N的Prepare请求。当然,也可以回复一个error,让Proposer尽早知道自己的提案不会被接受。
因此,一个Acceptor只需记住:1. 已接受的编号最大的提案 2. 已响应的请求的最大编号。
Pasox算法描述
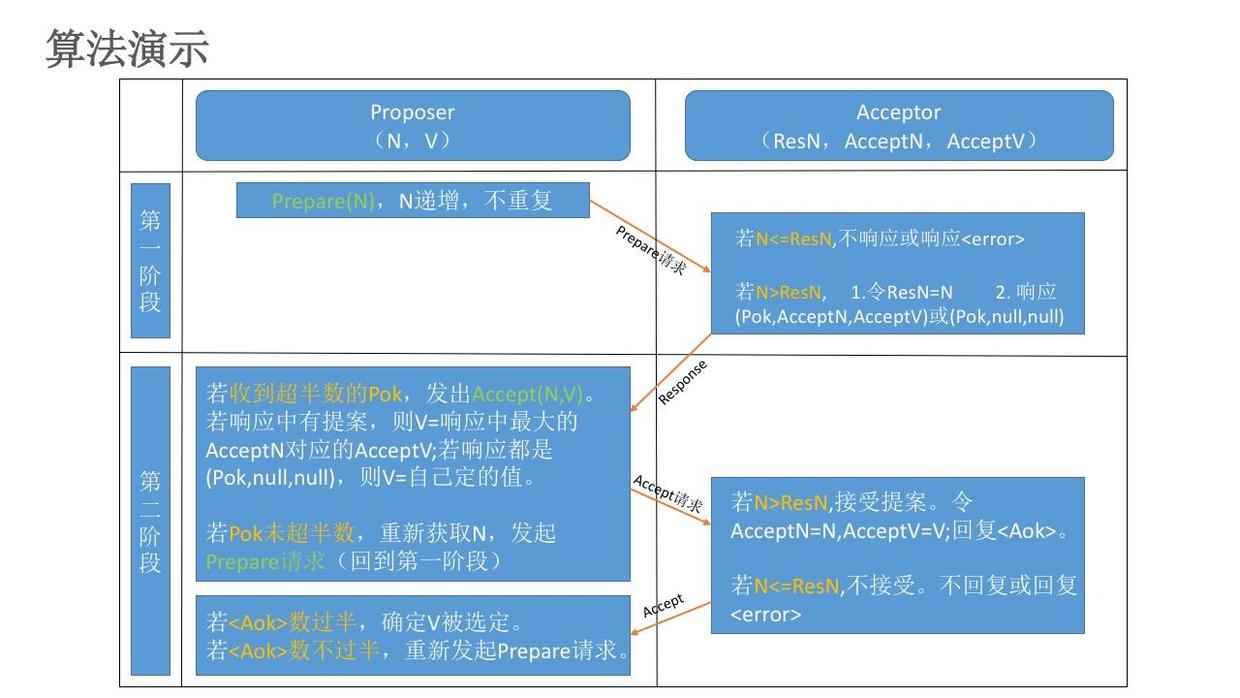
经过以上推导,现在对完整算法定义如下: Paxos算法可分为两个阶段:
1. Prepare阶段:
- Proposer选择一个提案编号n并将prepare请求发送给Acceptors中的一个多数派;
- 如果一个Acceptor收到一个编号为n的Prepare请求,且n大于该Acceptor已经响应过的所有Prepare请求的编号,那么它就会将它已经接受过的编号最大的提案(如果有的话)作为响应反馈给Proposer,同时该Acceptor承诺不再接受任何编号小于n的提案。
2. Accept阶段:
- 如果Proposer收到半数以上Acceptor对其发出的编号为n的Prepare请求的响应,那么它就会发送一个针对[n,v]提案的Accept请求给半数以上的Acceptor。注意:v就是收到的响应中编号最大的提案的value,如果响应中不包含任何提案,那么v就由Proposer自己决定。
- 如果Acceptor收到一个针对编号为n的提案的Accept请求,只要该Acceptor没有对编号大于n的Prepare请求做出过响应,它就接受该提案。
Learner学习被选定的value
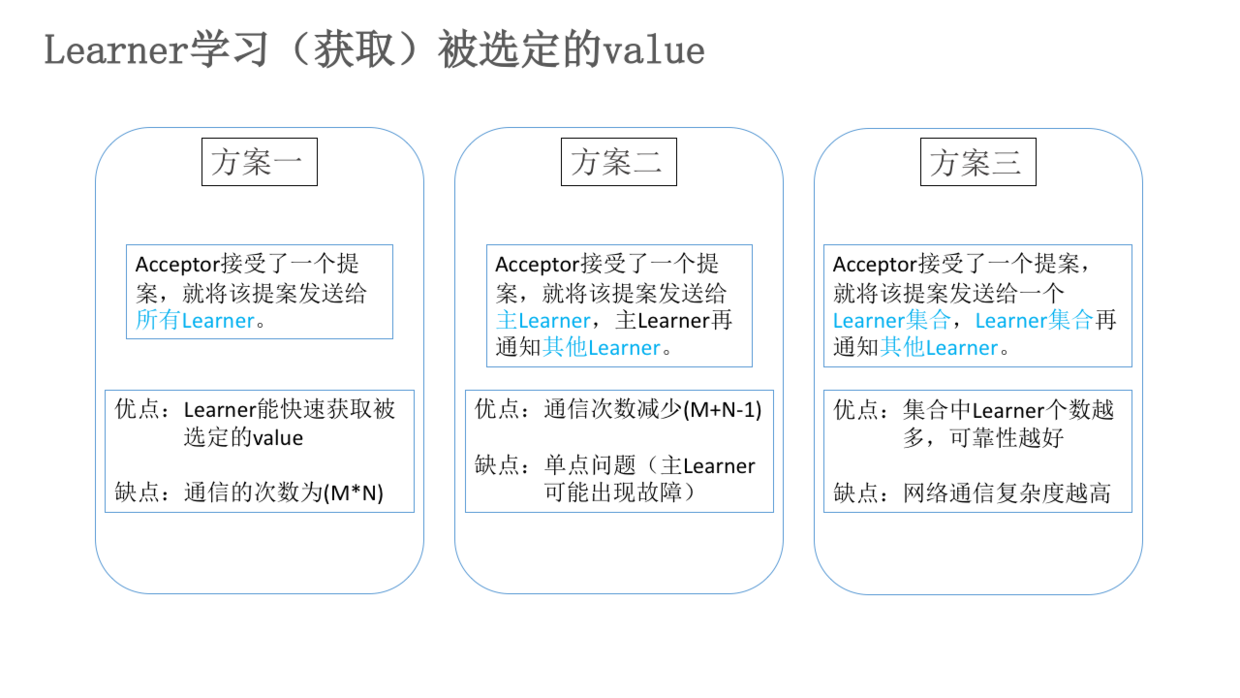
Learner学习(获取)被选定的value有如下三种方案:
保证Paxos算法的活性

通过选取主Proposer,就可以保证Paxos算法的活性。至此,我们得到一个既能保证安全性,又能保证活性的分布式共识算法——Paxos算法。
4. Multi-Paxos
4.1 概述
Paxos的典型部署需要一组连续的被接受的值(value),作为应用到一个分布式状态机的一组命令。如果每个命令都通过一个Basic Paxos算法实例来达到一致,会产生大量开销。
如果Leader是相对稳定不变的,第1阶段就变得不必要。 这样,系统可以在接下来的Paxos算法实例中,跳过的第1阶段,直接使用同样的Leader。
为了实现这一目的,在同一个Leader执行每轮Paxos算法时,提案编号 I 每次递增一个值,并与每个值一起发送。Multi-Paxos在没有故障发生时,将消息延迟(从propose阶段到learn阶段)从4次延迟降低为2次延迟。
4.2 消息流图形表示对比
Multi-Paxos没有失败的情况
在下面的图中,只显示了基本Paxos协议的一个实例(或“执行”)和一个初始Leader(Proposer)。注意,Multi-Paxos使用几个Basic Paxos的实例。
Client Proposer Acceptor Learner
| | | | | | | --- First Request ---
X-------->| | | | | | Request
| X--------->|->|->| | | Prepare(N)
| |<---------X--X--X | | Promise(N,I,{Va,Vb,Vc})
| X--------->|->|->| | | Accept!(N,I,V)
| |<---------X--X--X------>|->| Accepted(N,I,V)
|<---------------------------------X--X Response
| | | | | | |
式中V = (Va, Vb, Vc) 中最新的一个。
跳过阶段1的Multi-Paxos
在这种情况下,Basic Paxos的后续实例(由I+1表示)使用相同的Leader,因此,包含在Prepare和Promise的阶段1(Basic Paxos协议的这些后续实例)将被跳过。注意,这里要求Leader应该是稳定的,即它不应该崩溃或改变。
Client Proposer Acceptor Learner
| | | | | | | --- Following Requests ---
X-------->| | | | | | Request
| X--------->|->|->| | | Accept!(N,I+1,W)
| |<---------X--X--X------>|->| Accepted(N,I+1,W)
|<---------------------------------X--X Response
| | | | | | |
5. 参考资料
- 论文《Paxos Made Simple》
- 论文《The Part-Time Parliament》
- 英文版维基百科的Paxos
- 中文版维基百科的Paxos
- Paxos算法原理与推导